参考書：多変量解析法入門
サイエンス社「多変量解析法入門」（黄緑本）。各章ごとに冒頭で解析ストーリーの全体像から説明してくれる構成がとてもわかりやすく、統計学のひと通りの基礎（統計検定2級レベル）を押さえてからもう少し多変量解析分野を掘り下げたいときにうってつけの参考書である。
上記参考書の例題をもとに、紙とエンピツだけでなくstatsmodelsライブラリを用いて計算結果を確認してみる。
単回帰分析（黄緑本第4章）
回帰式をつくる
必要ライブラリのインポート。プロットする際の文字化け（豆腐化）を解消するためにjapanize_matoplotlibを用いる。
import pandas as pd
import statsmodels.formula.api as smf
import statsmodels.stats.outliers_influence as smf_i
import matplotlib.pyplot as plt
import seaborn as sns
import japanize_matplotlib※サンプルデータ（含有量x, 収率y）は参考書を参照
まずはサンプルデータのcsvを用意し、データを読み込む。
df = pd.read_csv('data_1_単回帰分析.csv')
df.head()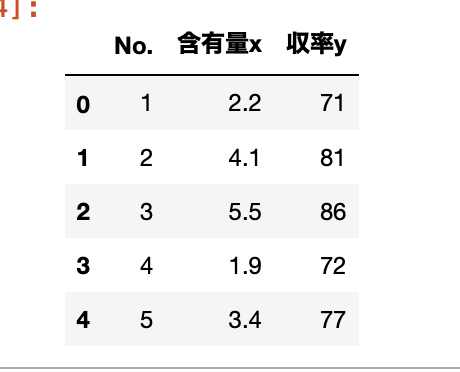
データを散布図にプロットする。
plt.plot(df[['含有量x']], df[['収率y']] , 'o')
plt.xlabel('含有量x')
plt.ylabel('収率y')
plt.show()説明変数と目的変数の間にかなり強い正の相関が見られる。
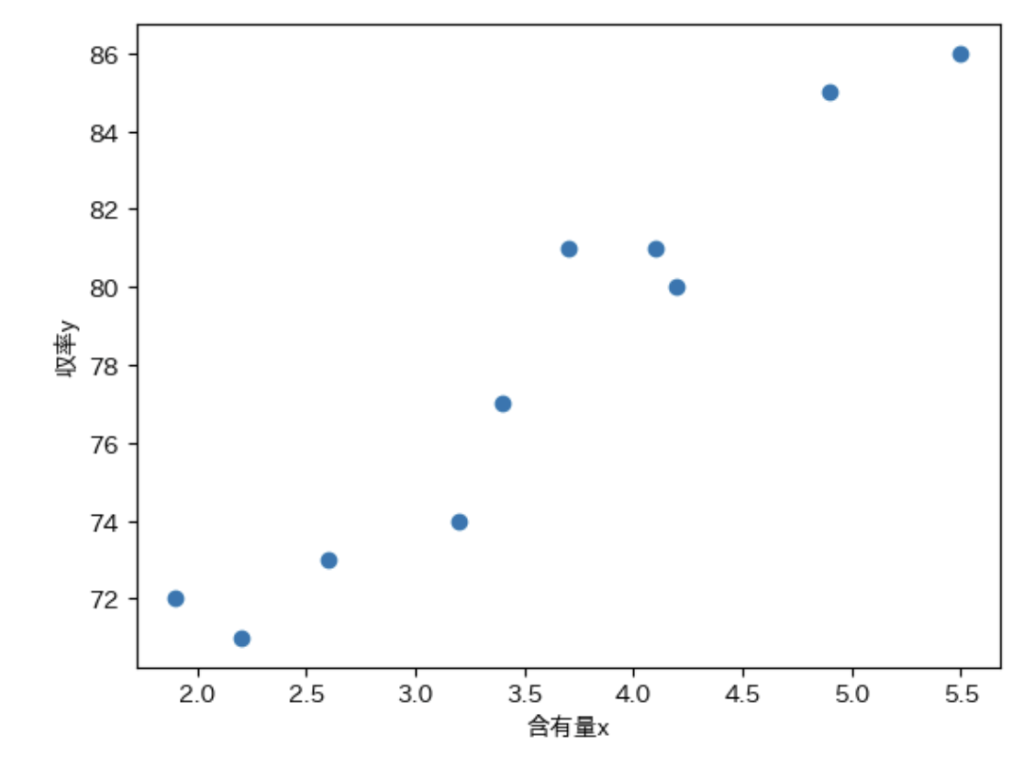
回帰式を作る変数セットをformulaに’y ~ x’の形で格納し、formulaをsmf.olsに渡してmodelをつくる。
formula = '収率y ~ 含有量x'
model = smf.ols(formula, df)model.fit()で回帰式を計算して、model.summary()で回帰分析の結果を表示する。
results = model.fit()
results.summary()summaryが一覧になって表示される。
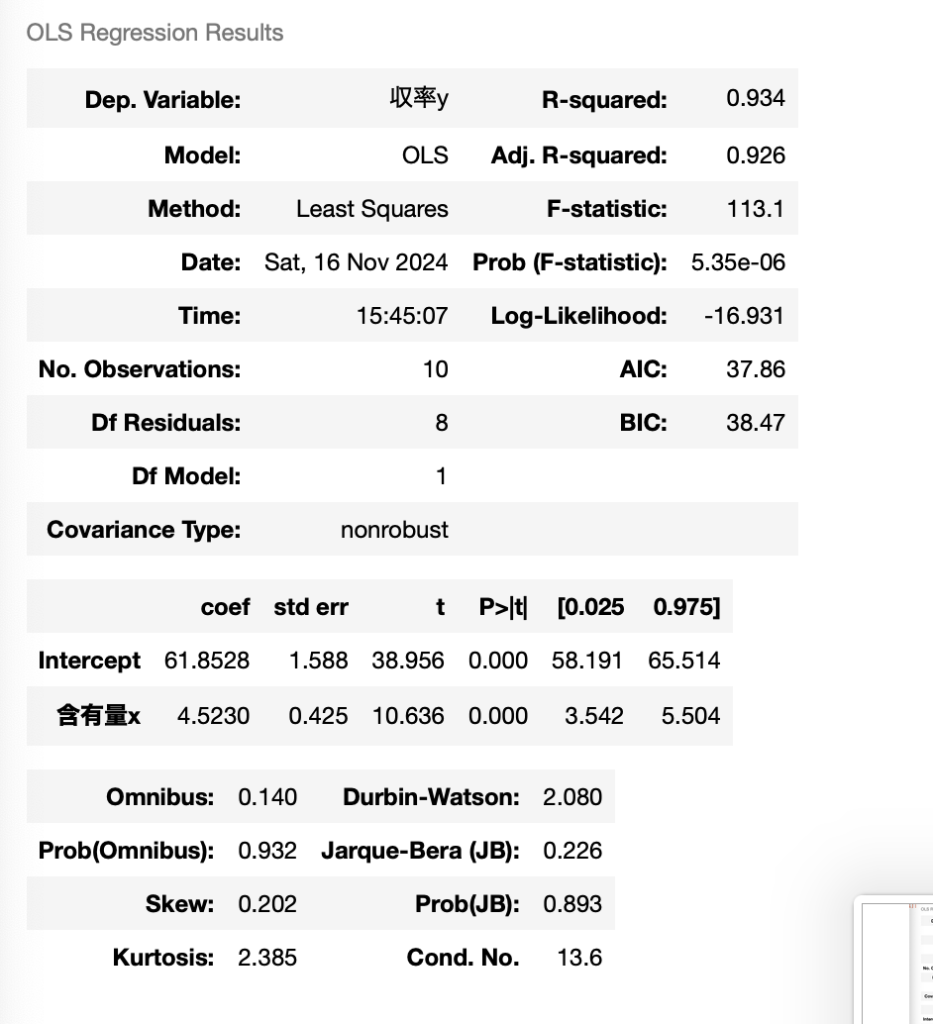
summaryを読む
・2段目：Interceptのcoefがβ0、含有量xがβ1になる。
→求める単回帰式はy = 61.8528 + 4.5230x。
・1段目：R-squaredが寄与率、Adj.R-squaredが自由度調整済寄与率になる。
→R^2 = 0.934、R^*2 = 0.925。
・2段目：含有量xのtがβ1の検定量になる。
→t0 = 10.636 > t(8,005)なのでβ1は有効と判断する。
・2段目：含有量xの[0.0025 0.975]がβ1の95%信頼区間になる。
→95%信頼区間：3.542 , 5.504。
以上について、参考書4章例題1の計算結果とほぼ一致することを確認した。
テコ比（の代わりにCookの距離）
statsmodelsではテコ比を返してくれる処理が見当たらなかったので（もっと探せばあるかも）、テコ比の発展型であるCookの距離をstatsmodels.stats.outliers_influenceオブジェクトのcooks_distanceを用いて確認してみる。（統計WEBの解説）
olsinf = smf_i.OLSInfluence(results)
olsinf.cooks_distance得られたCookの距離。値が0.5を超えると外れ値として疑う必要があるが、サンプルについては特に異常値無しと判断する。※参考書記載のテコ比も異常値無し。
β1の検算をしてみよう
単回帰式の傾きにあたるβ1はresults.summaryで一発で求まるが、念のためβ1=Sxy/Sxxを手計算で確認してみる。
まずは平方和Sxxから求める。
#xの平均値x_mean
x_mean = df['含有量x'].mean()
#x_mean=3.5700000000000003
#xの偏差x_dif
df['x_dif'] = df.apply(lambda x: x['含有量x'] - x_mean, axis=1)
df['x_dif']
#x_difの二乗x_dif_s
df['x_dif_s'] = df.apply(lambda x: x['x_dif'] ** 2, axis=1)
df['x_dif_s']各データのxの偏差の二乗。Sxxはこれらの和を取れば良い。
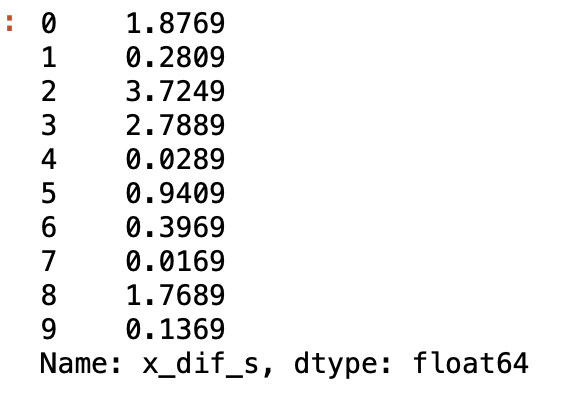
#xの平方和Sxx
Sxx = df['x_dif_s'].sum()
Sxx
#Sxx=11.961同様に偏差積和Sxyを求めていく。
#yの平均y_mean
y_mean = df['収率y'].mean()
#y_mean=78.0
#yの偏差y_dif
df['y_dif'] = df.apply(lambda x: x['収率y'] - x_mean, axis=1)
#xとyの偏差積xy_dif
df['xy_dif'] = df.apply(lambda x: x['x_dif'] * x['y_dif'], axis=1)
各データのxとyの偏差の積。これらの和をとって偏差積和Sxyが求まる。
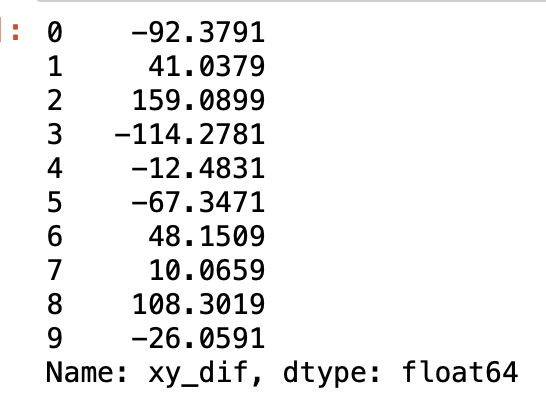
#xとyの偏差積和Sxy
Sxy = df['xy_dif'].sum()
#Sxy=54.09999999999984最終的にβ1=Sxy/Sxxを計算するとβ1≒4.5230となり、results.summaryで取り出したβ1と一致することを確認できた。
#β1の推定値beta1_hat
beta1_hat = Sxy/Sxx
#beta1_hat=4.5230331912047355ちなみに、resultsオブジェクトの中身をpy4macroで見てみると以下の一覧の通りとなる。
py4macro.see(results)
SxxとSxyをこの中から直接取り出せれば尚良かったが、少し探した限りでは無さそうだった。（ちゃんと掘ればあるかも）
※Syyはresults.centered_tssで取り出せる。
以上
