参考書:多変量解析法入門(サイエンス社)
各章ごとに冒頭で解析ストーリーの全体像から説明してくれる構成がとてもわかりやすく、統計学のひと通りの基礎(統計検定2級レベル)を押さえてからもう少し多変量解析分野を掘り下げたいときにうってつけの参考書。

多変量解析法入門
上記参考書の例題をもとに、紙とエンピツだけでなくscikit-learnライブラリを用いて計算結果を確認してみる。
主成分分析(黄緑本第9章)
データ作成から標準化まで
必要ライブラリのインポート。プロットする際の文字化け(豆腐化)を解消するためにjapanize_matoplotlibを用いる。
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.decomposition import PCA
from sklearn.preprocessing import StandardScaler
import japanize_matplotlib
import py4macroサンプルデータのcsvを用意して読み込む。
※データの内容は黄緑本9章を参照
df = pd.read_csv('data_9_主成分分析.csv')
df.head()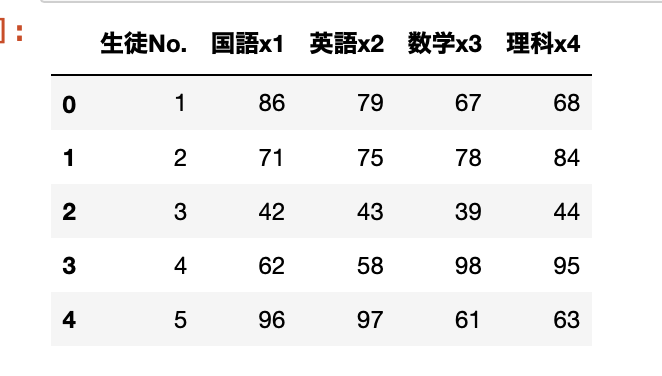
ヒートマップを出して相関を見ておく。
df_corr = df[['国語x1','英語x2','数学x3','理科x4']]
corr = df_corr.corr()
sns.heatmap(corr, annot=True)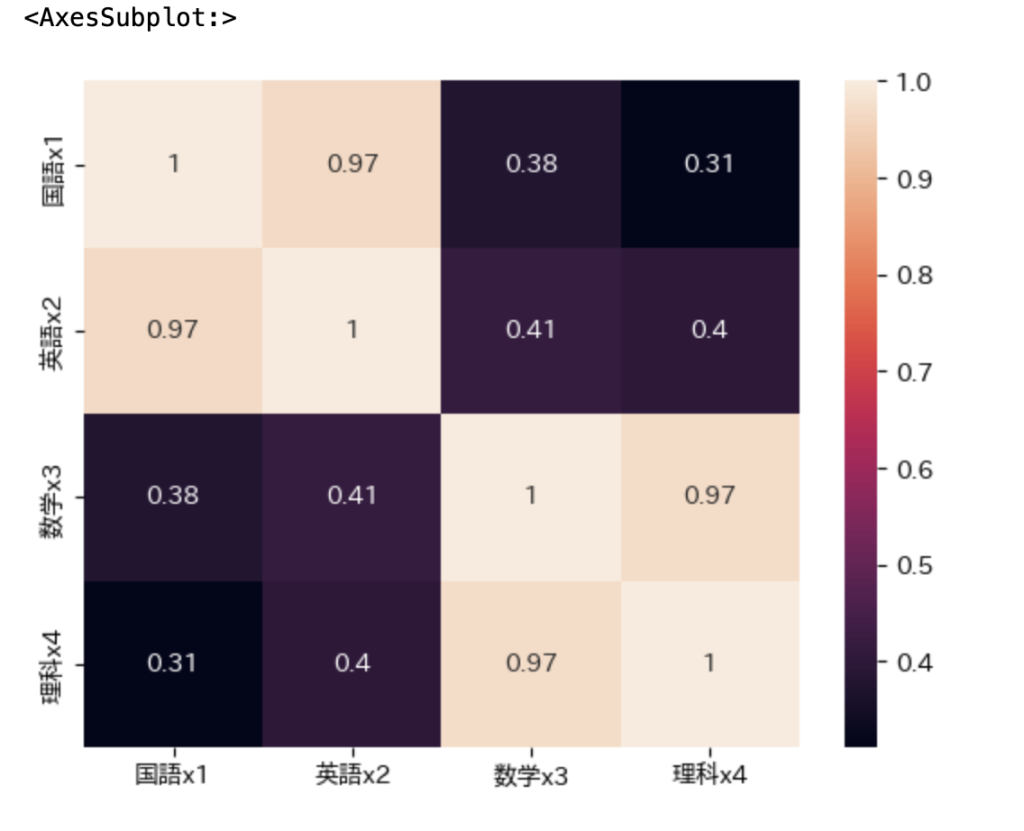
各変数を標準化する。
X = df[['国語x1','英語x2','数学x3','理科x4']]
scaler= StandardScaler()
X_ss = scaler.fit(X)
#scaler.transform(X)
X_ss = pd.DataFrame(scaler.transform(X), columns=X.columns)
X_ss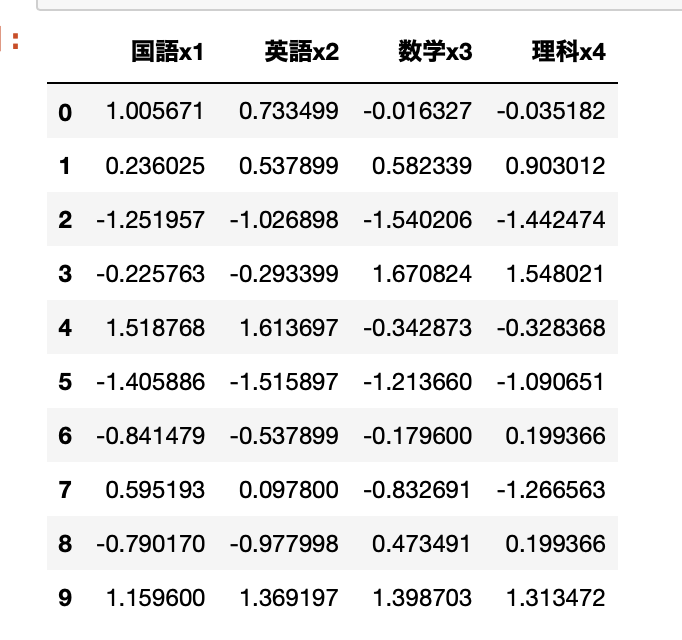
主成分分析の実行、主成分と因子負荷量のプロット
主成分分析を行うオブジェクトpcaを生成する。主成分数n_componentsは2次元を指定する。
pca = PCA(n_components=2)主成分を計算する。2次元のリストで返ってくるのでdfに変換する。
temp = pca.fit_transform(X_ss)
df_z = pd.DataFrame(temp, columns = ['z1','z2'])
df_z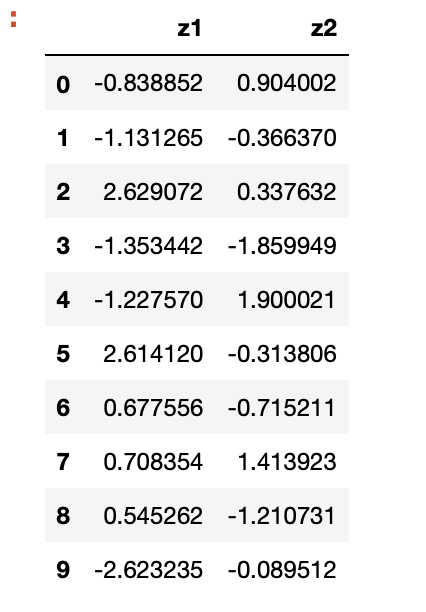
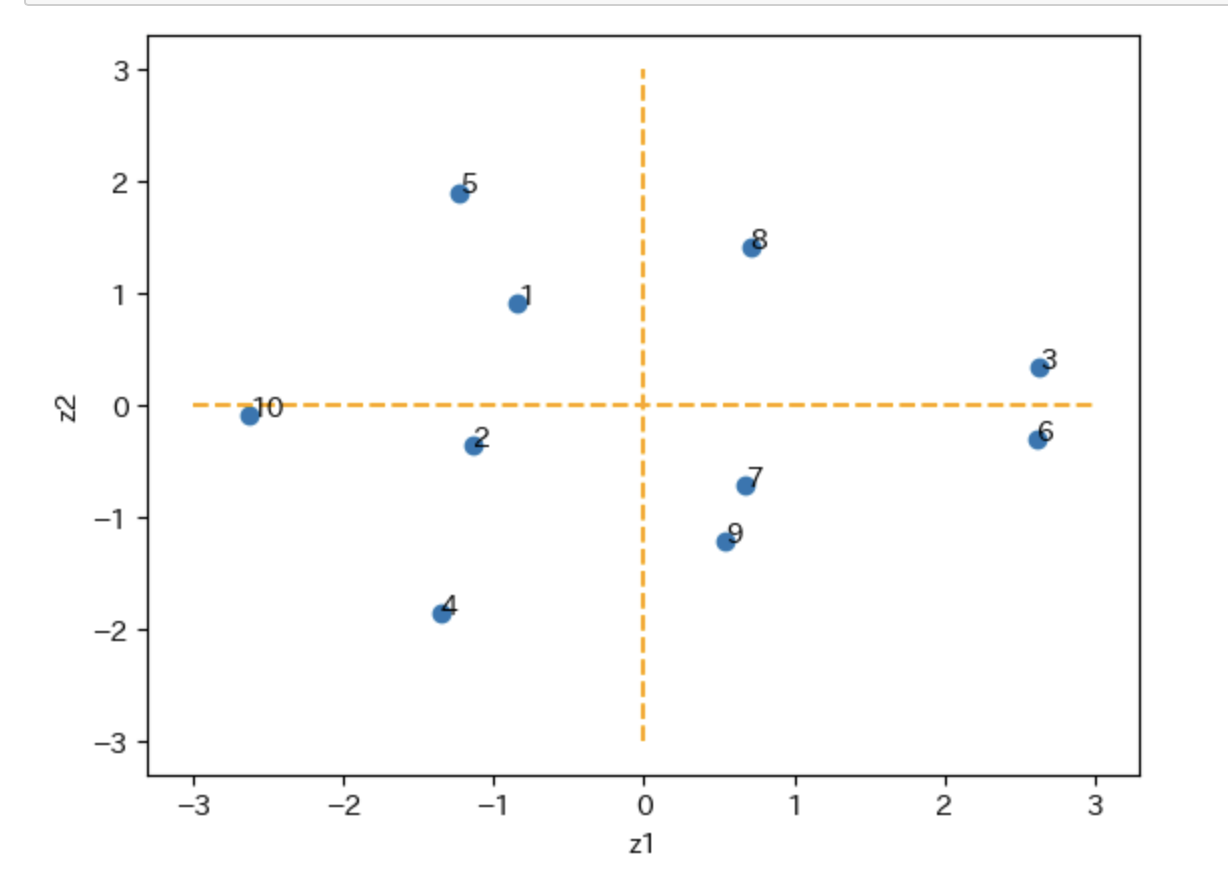
計算した主成分を散布図にプロットする。
xmin, xmax = -3,3
ymin, ymax = -3,3
#データラベル用のリストを用意する
labels = df['生徒No.'].values.tolist()
labels = list(map(str,labels))
x_list = df_z['z1'].values.tolist()
y_list = df_z['z2'].values.tolist()
#描画
plt.plot(df_z[['z1']], df_z[['z2']] , 'o')
plt.xlabel('z1')
plt.ylabel('z2')
plt.hlines([0], xmin, xmax, "orange", linestyles='dashed')
plt.vlines([0], ymin, ymax, "orange", linestyles='dashed')
#データラベルの描画
for _x, _y, label in zip(x_list, y_list, labels):
plt.text(_x, _y, label)
plt.show()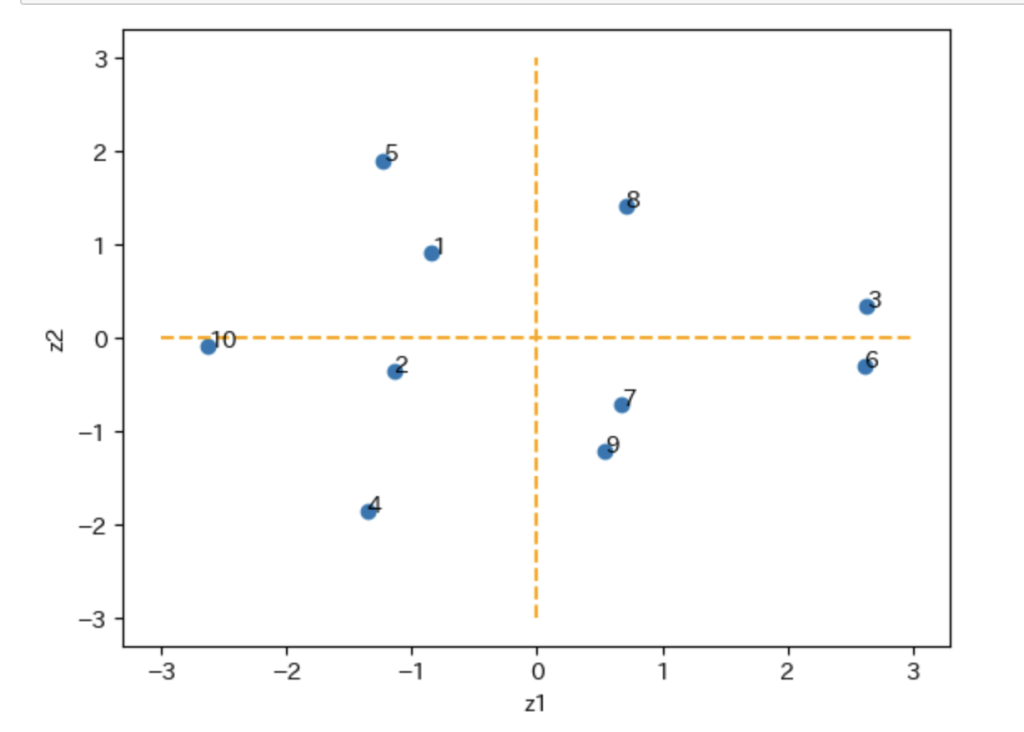
因子負荷量を計算する。
df_load = pd.DataFrame(
pca.components_.T,
columns=[f'PC{i}' for i in range(1, len(pca.components_) + 1)],
index=X_ss.columns)
df_load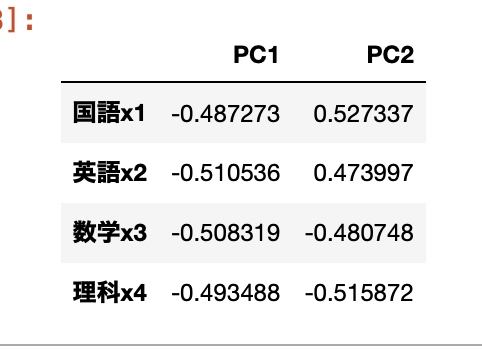
因子負荷量をプロットする。
xmin, xmax = -1,1
ymin, ymax = -1,1
#データラベル用のリストを用意する
labels = df_load.index.values.tolist()
labels = list(map(str,labels))
x_list = df_load['PC1'].values.tolist()
y_list = df_load['PC2'].values.tolist()
#描画
plt.plot(df_load[['PC1']], df_load[['PC2']] , 'o')
plt.xlabel('z1')
plt.ylabel('z2')
plt.hlines([0], xmin, xmax, "red", linestyles='dashed')
plt.vlines([0], ymin, ymax, "red", linestyles='dashed')
#データラベルの描画
for _x, _y, label in zip(x_list, y_list, labels):
plt.text(_x, _y, label)
plt.show()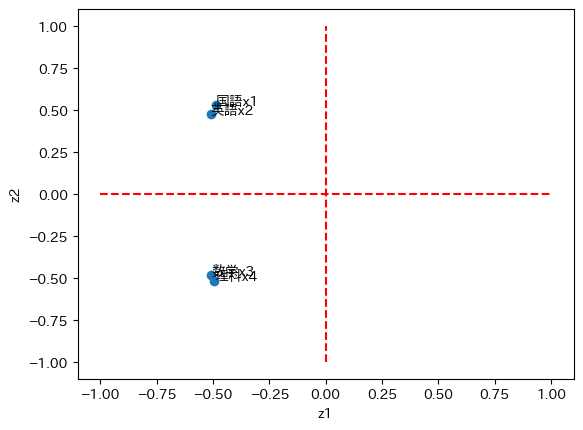
解釈
第一主成分は全ての変数が負になっているので、第一主成分が負に大きいほど総合学力が高いと読み取れる。
第二主成分は国語と英語が正、数学と理科が負になっているので、第二主成分が正であれば国語と英語が得意、負であれば数学と理科が得意であることが読み取れる。
参考書のプロットと比較するとそれぞれy軸を対象にデータのプロットが反転してはいるが、データに対する主成分分析、因子負荷量の傾向はそれぞれ同じ解釈になることを確認できた。
以上