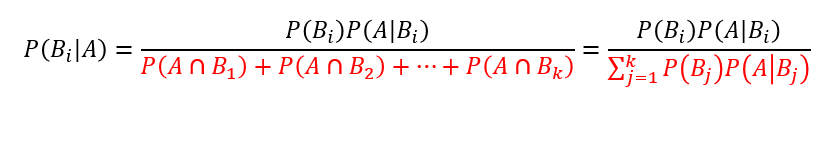世の中の男が高確率で体験したことがあるであろう「アレ」
彼女ができるには?難しいよね。紹介、合コン、マッチングアプリ、正解がないと思うよ。
でも俺、負けないよ。(何に?)
上記のいずれの方法にしても、関係を進めるために必要なのは「初回または次回以降、相手とデートする予定を取り付ける」ことであるのだが、往々にして以下のようなやり取りが発生したりするものである。

今度ご飯にでも行きましょ~!

ぜひぜひ~!

◯◯日はどうですか? or いつ頃がご都合よいですか~?

ん~、ちょっと今忙しいので予定がわかったらまた連絡しますね!
このようなやり取りを経験した人であれば、この後の展開の大半がフェードアウトであることを理解されているかと思うが、今回はこの現象をベイズの定理を使用して考えていく。
ベイズの定理
ベイズの定理についての説明は以下のサイトがわかりやすいのだが、簡単に言うと「現象Aと現象Bがそれぞれあり、現象A(結果)が起きたとき現象B(原因)のうち特定の原因Biである確率を求める」ものである。(ややこしい)

このベイズの定理を用いて、
現象A:「忙しいのでまた連絡しますね~」という連絡が来た
である場合、
現象Bi:脈あり(実際に忙しく、当面の予定が本当につかないだけ)
である確率を考えていく。
前提
脈ありである確率は以下のサイトを参考に、男女同値として20%を想定する。(なんかそういうデータあるんすか?)

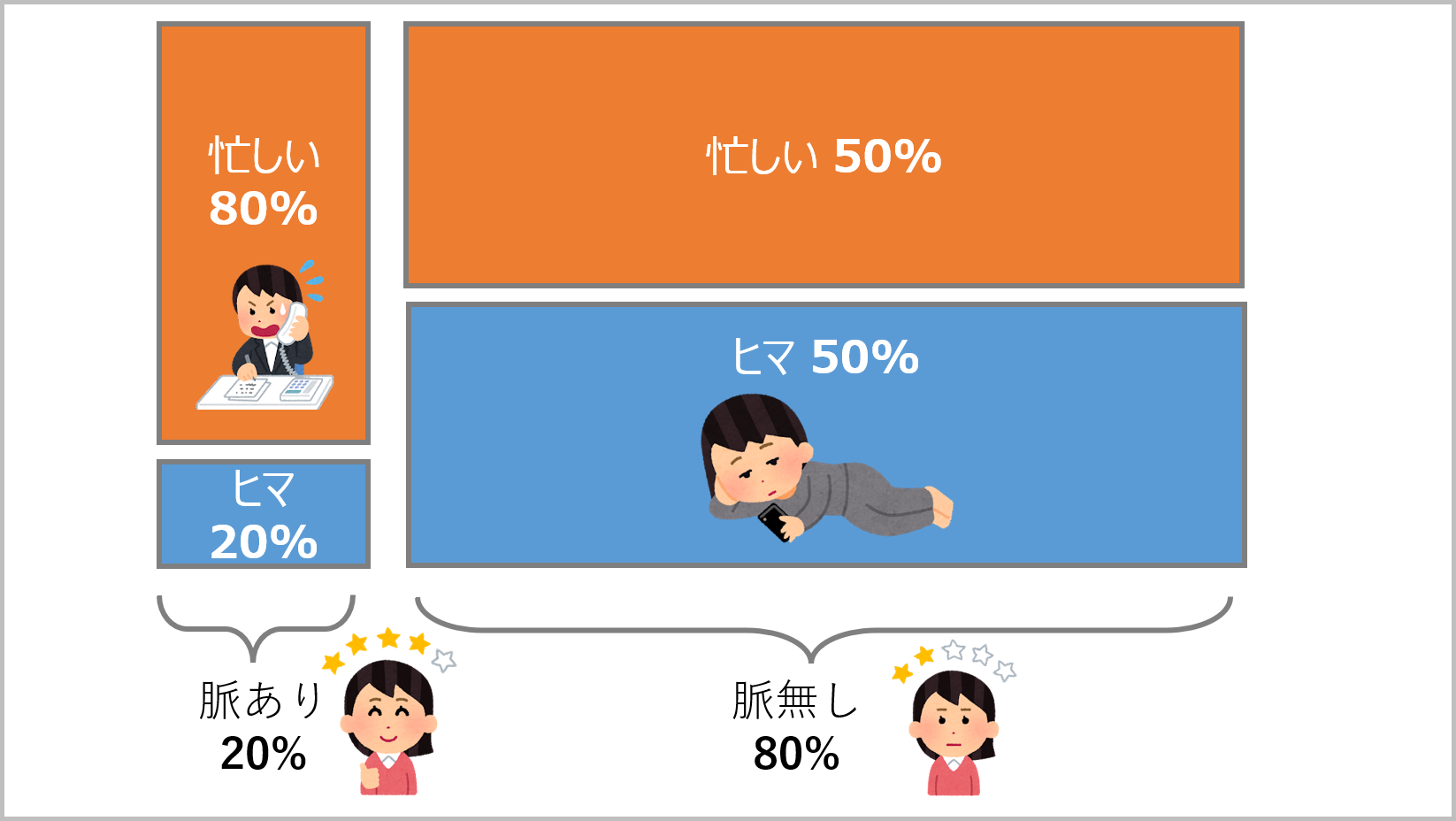
事象B:脈あり(B1):20%、脈無し(B2):80%
事象B1のうち、忙しい確率(A1):80%、ヒマな確率(A2):20%
事象B2のうち、忙しい確率(A1):50%、ヒマな確率(A2):50%
図にすると以下のようなイメージになる。
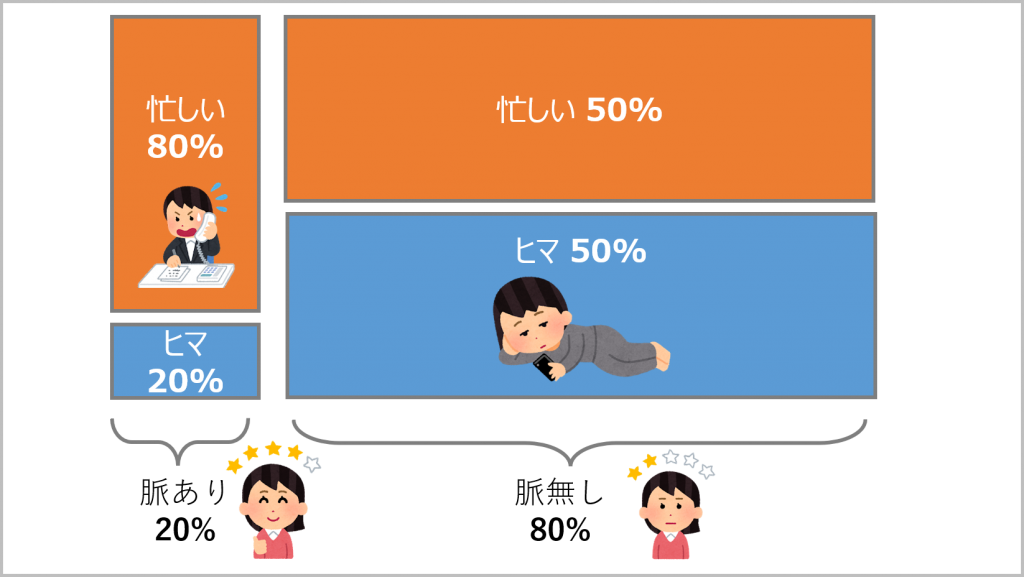
前提をベイズの定理に適用する
今回はそれぞれの事象をシンプルに2要素で分けて考えるので、以下の式に各要素をぶちこんで計算していく。
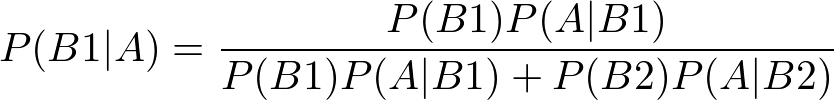
| 事象 | 数式上の事象 | 確率 |
| 脈ありである | P(B1) | 0.2 |
| 脈ありの条件のもとで、相手が本当に忙しい | P(A|B1) | 0.8 |
| 脈無しである | P(B2) | 0.8 |
| 脈無しの条件の下で、相手が本当に忙しい | P(A|B2) | 0.5 |
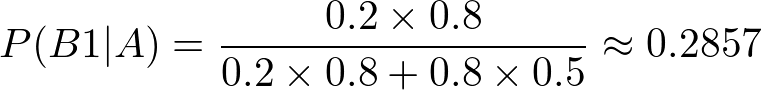
結論
相手から「忙しいのでまた連絡しますね~」という連絡が来たとき、
脈ありである確率は約28.5%となる。…意外と高いな!(限界男子の感想)
おわり