炎上
2021年11月6日、明治安田生命J1リーグの横浜・F・マリノス対FC東京は8-0という衝撃的なスコアとなった。
これに対し某東京都都議がFC東京の惨敗を「ありえないスコア」と形容し、このような敗けをさらすようでは長谷川健太監督の辞任は当然とイキリ散らかした喝破した(ついでに中盤の補強を要求した)ものの、どうも主張にズレ感があったのか異議を唱えるリプライが殺到、炎上騒ぎとなった。
日頃のJリーグを見ているサポーターの方であれば8-0が「あり得ない」というのにはやはり違和感を感じるものであるが、数字で客観的に見たときに本当にあり得ないのか?を調べてみた。
調べてみた
試合データは例によりJリーグデータサイトより、1998-2021シーズンのJ1リーグ計6992試合を対象とした。発言の要旨からして8-0というスコアそのものより、「8点差」ということがミソだと解釈し、各試合の「点差」を集計して評価した。
結果
点差の分布は以下のようになった。
| 点差 | 試合数 | 割合(%) |
| 0 | 1463 | 20.9 |
| 1 | 3141 | 44.9 |
| 2 | 1427 | 20.4 |
| 3 | 605 | 8.65 |
| 4 | 239 | 3.42 |
| 5 | 78 | 1.12 |
| 6 | 23 | 0.239 |
| 7 | 12 | 0.172 |
| 8 | 4 | 0.0572 |
棒グラフは以下の通り。
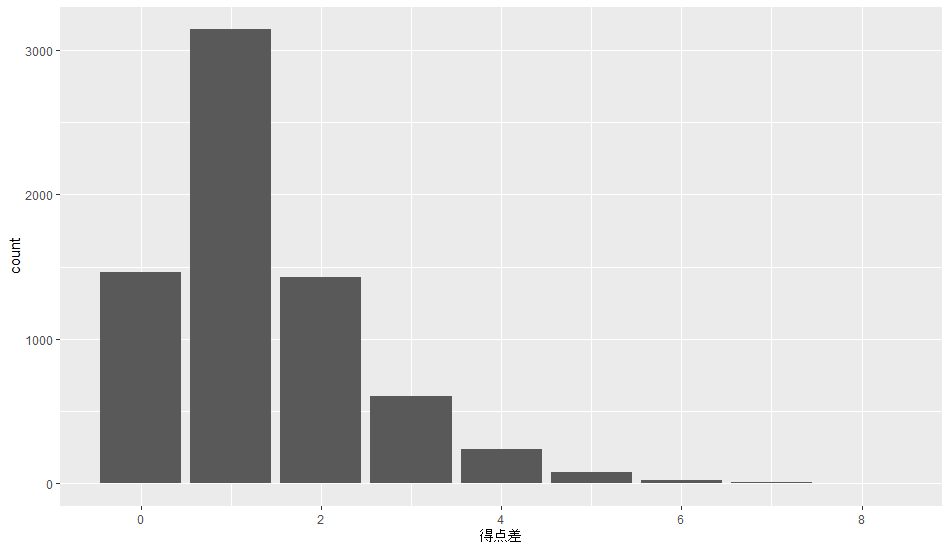
「ありえない」スコアなのか?
以上より、8点差のゲームは全体の0.0572%となった。これがあり得ないスコアなのか?
統計に詳しい愚地独歩先生の見解は以下の通り。

0.0572% > 30万分の1なので、それが起こる可能性は「ある」。
結論
8-0は「ありえないスコア」ではない。
Rでの実装
library("tidyverse")
score_J1 <- read_csv("./score_j1.csv") %>%
select(得点差)
#得点差の度数
score_J1 %>%
table()
#得点差の相対度数
score_J1 %>%
table() %>%
prop.table() * 100
#得点差のグラフ
ggplot(data = score_J1) +
geom_bar(aes(x = 得点差))

